Categories: school
Written by Stefan Nikolaj
01 Apr 2022

---

Imagine you’re doing a chemistry exam, and you’re at the last question. You’ve forgotten about the passage of time, you’ve forgotten about anything else except for a song that’s stuck in your head and looping repeatedly, and suddenly you see a question that asks you to balance this equation:

__C₂H₇N + __O₂ → __CO₂ + __H₂O + __N₂

However, unfortunately, the last of your brain cells are either exhausted or eliminated, and you forgot how the process of balancing goes… Well, here I present to you a small and simple method to balance equations that will make sure you never have to think or fail an exam. It just involves a bit of practice, and then you’ll never forget it. To demonstrate, I will use a TI-84 Plus CE graphing calculator, however it’s possible to use this method even without a calculator, though having one makes it significantly easier. I will first outline the steps needed, and then provide a condensed version with mnemonics so that you can easily remember it.

Detailed procedure:

• Take note of the number of compounds and different elements in your equation. In our case, we have 5 compounds (C₂H₇N, O₂, CO₂, H₂O, N₂) and 4 elements (C, H, N, O).

• Assign each compound a variable, in our example we will get aC₂H₇N + bO₂ → cCO₂ + dH₂O + eN₂

• Draw a table with dimensions compound x element and populate it according to this example:

	C2H7N	O2	CO2	H2O	N2
C
H
N
O

  In other words, have the column identifiers correspond to each compound, and the row identifiers to each element.

• Now, populate the table according to how many of the elements in the row are present in the compounds in the column, or in our example:

	C2H7N	O2	CO2	H2O	N2
C	2	0	1	0	0
H	7	0	0	2	0
N	1	0	0	0	2
O	0	2	2	1	0

• Now, there are two ways to proceed. First, we have to recognize that what we have here is a system of equations represented in matrix form. We can write out this table as a system of equations according to all the variables we assigned each compound, where the equals sign will correspond to the arrow symbol, or:
  2a = c
  7a = 2d
  a = 2e
  2b = 2c + d
  As you can see, there are as many equations as there are elements. Now, you can choose to solve this as a normal system of equations, either by hand or by an advanced graphing calculator (like the TI Nspire-II). Or, if you have a TI-84 Plus CE like me, you can follow these optional steps:
  1. Go to apps → PlySmlt2 (9) → SIMULTANEOUS EQN SOLVER (2).
  2. For EQUATIONS select how many elements there are (in our case 5) and for UNKNOWNS select how many compounds there are (in our case 4).
  3. Now you have to enter the table, however (important!) make sure to make each variable after the arrow negative, since we are essentially moving all variables to one side to make the other side equal to zero.
  4. Now we have:
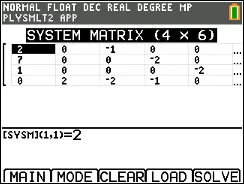
     Your table should look like this, and now press SOLVE (graph button) to get this screen:
  5. (Almost) final solution:
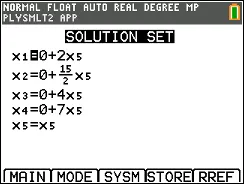
     This is the solution! Each x corresponds to each letter variable we assigned to our compounds. If you solved by hand, you should also get the same result.
• Now, whether you solved by hand or TI-84, you should be able to express each variable through one (x₅ in the case of the TI-84). The last step you need to do is multiply each equation by a number needed to remove all fractions or decimal numbers. In this case, for x₂ there is a 15/2 we need to eliminate, so multiply all sides 2 to get:
  x₁ = 4x₅
  x₂ = 15x₅
  x₃ = 8x₅
  x₄ = 14x₅
  x₅ = x₅
  Now just replace each x for the variable it represents (if you used the TI-84 method) and if you have whole numbers for each relationship, just replace the variable you used to represent it with 1. In my case, I put x₅ to be 1 and get the final solution:
  aC₂H₇N + bO₂ → cCO₂ + dH₂O + eN₂
  4C₂H₇N + 15O₂ → 8CO₂ + 14H₂O + N₂

Now, even if this method appears to be long, with only a few minutes of practice you can cut out the step with the table completely and just input the numbers by sight into the calculator, which means that you can balance equations correctly every time, with no effort, in less than a minute. To recap:

1. Write down number of compounds and elements
2. Make table for compounds x elements
3. Input amount of each element in each compound for the corresponding cell
4. Make system of equations
5. Solve system of equations
6. Copy result